Post by KenPost by MatsSom komplement till Torbjörns detaljerade genomgång nedan
kan det vara värt att läsa
http://www.epanorama.net/documents/wiring/cable_impedance.html
Enligt detta är inte 100 Ohm så fel.
För mitt eget bruk blir 100 Ohm alldeles perfekt eftersom de
IC jag tänker använda kommer att må bra av 100 Ohm på utgången.
100 Ohm verkar vara ett bra värde i mitt fall.
(efter som jag övh. skriver här så innebär att dom elektriska hornen
har växt ut - om ni inte vill läsa mina utlägg impedanser och
LF-frekvenser så kan ni sluta läsa här!)
Dock gör man felet, som nästa alla andra, att man nämner
att impedanserna är anorlunda vid LF-tonfrekvenser och snabbt
hoppar upp till > 200 KHz i vidare disskusionen utan att markera
att nu pratar vi HF och inget annat... - dom 100 Ohm:en gäller
alltså inte för Audio, men å andra sidan så är sträckorna inte så långa
heller i HiFi-sammanhang och man kan betrakta kabeln som en kapacitans
mot jord. Det intressanta är då längden samt hur många pF/m kabeln
har och därmed dess sammanlagda kapacitans.
Om man verkligen är angelägen så kan anpassa utgångsstegets impedans
så att den hanterar och kompenserar för kapasitiv last, kanske med en
kondensator av lämpligt värde (beroende av kabellängden) parallellt över
utgångsmotståndet för att behålla pulsutseendet på signalen
- om utgångssteget (OP-ampen) klarar av det utan att självsvänga och
ringa...
Den tekniken används bl.a. på oscilloskopprobar med sin vrid-
kondensator för att ratta in bästa möjliga fyrkantvåg och handlar
egentligen om kapacitiv spänningsdelning parallellt med den
resistiva dito. dvs.
R1 1 kOhm R2 10 kOhm
____ _____
----|____|----------oo------------------oo-----------|_____|----
| | | |
| || | | C2 | Cp
|---||---| ----- -----
|| ----- ----- (okänd parasit
C1 10 nF | kabel- | kondensator =0pF)
| kapacitans |
| (1nF = ca 18m |
| kat5 kabel) |
--------------------oo------------------00----------------
utgångsdel kabel ingångsdel
(här modulerat på utgången av OP-amp NE5532, 1k serieresistans på
utgången och i ovan exempel dessutom parallellkondensator C1 a 10 nF
för kompensation av kabelkapacitans av totalt 1nF (52pF/m)
samt en resistiv ingångsteg a 10 kOhm.)
Här får man den (o)roliga effekten att resultatet blir sämre
när man ökar C1 från 0 -> 2 nF för att sedan bli bättre och
vid 10 nF är det fullt kompenserat inom hela aktuella
frekvensområde. Vidare så ser man att ju lägre utgångsimpedans R1,
ju större parallellkapacitans måsta man använda då kvoterna mellan
utgångsimpedans och ingångsimpedans måste behållas i systemet.
Utan kompensationskondensator så får man ca 0.07 dB lägre nivå
vid 22kHz än vid 100 Hz på 10 m kabel.
Mao. ingenting att ligga sömnlös för om man inte hör till dom där
Audiofilerna som måste ha allt perfekt... - dock när man ser hur en
pulståg eller fyrkantvåg (10 KHz) distas vid okompenserad koppling redan
efter 10 meter kabel så är man inte riktigt lika säker längre...
se längre ned:
vidare:
I spice-simulatorn så kunde jag inte låta bli och se vad som händer
när man skarvade en bunt 1m-bitar av kat-5 kabel, simulerat som:
0.188 Ohm
____
o-------|____|--------o
|
|
===== 58 pF efter varandra
|
|
o---------------------o
Med 1kOhm sändningsimpedans och 10 kOhm lyssningsimpedans
resultatet:
-----------------------------------------------------------------------
| längd |100 Hz | 22000 Hz | delta dB 100 Hz - |parallell kond C1|
| | | | 22000 Hz |för kompencering |
-----------------------------------------------------------------------
10 -0.831 dB -0.848 dB -0.018 dB 5.1 nF
20 -0.831 dB -0.905 dB -0.074 dB 10.4 nF
100 -0.843 dB -2.4 dB -1.56 dB 51.97 nF
500 -0.930 dB -11.78 dB -10.88 dB 285.6 nF
Med paralellkapacitans C1 enligt ovan så blir det helt frekvensrakt
inom 0.01 dB - dB-förbättringarna är inte så imponerande (förrän vid
långa kablar), men det som verkligen syns är
transientegenskaperna/flankerna på en fyrkantvåg. Från att ha varit
avrundade så blir dom så skarpa som OP-ampens slewrate förmår
- att de har blivit skarpa innebär också att man har rättat
till fasgången - sådana detaljer som inte lämnar audofilen
någon ro...
simulerat enl:
<
Loading Image...
>
för 10 meter kabel:
<
Loading Image...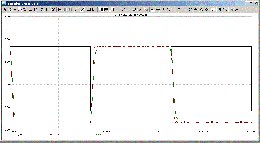
>
<
Loading Image...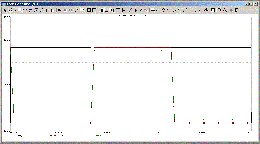
>
20 meter:
<
Loading Image...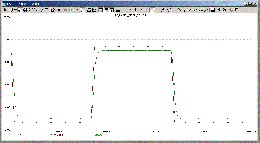
>
<
Loading Image...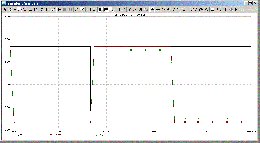
>
100 meter:
<
Loading Image...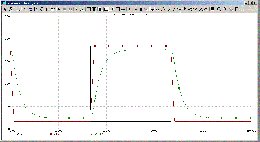
>
<
Loading Image...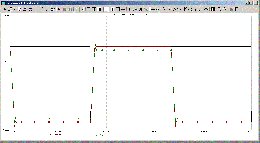
>
och slutligen rejält med 500 meter:
<
Loading Image...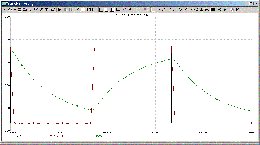
>
<
Loading Image...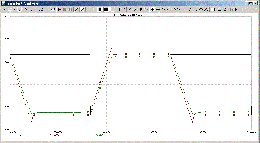
>
Man ser att det är OP-ampens strömförmåga som begränsar vid stora
längder... dock här tillräckligt bra för att köra 22kHz över 500 meter
Cat-5 utan diskantdämpning - om den kompenseras med parallellkondensator
över utgångsmotståndet C1.
Sträckorna över 100 meter skall man ta med en nypa salt, dels för
numeriska fel i spice pga. 100-tal RC-länkar efter varandra, dels för
att modellen med diskreta komponeneter utan avstånd mellan inte
håller riktigt längre när det börja få utsräckning i rummet.
så, vi gör en reality check - hur ser RG174 ut? (finns modell i simulatorn)
den tycker 30 nF C1 är en lämplig värde för 100 meter,
och 187nF efter 500m...
OK - Cat-5 kabel då?:
Se utredning [1] med resultatet vid 1 MHz - allt detta jobb för att
få fram alla kabelns 4 primärkonstanterna:
framberäknat @ 1 MHz uppgivet
längsmedresistansen R = 376 Ohm/Km (skin-effekt) 188 Ohm/km (DC)
paralellkapacitans C = 49.75 nF/km 52 nF/Km
längsmedinduktansen L = 0.4975 mH/km ej uppgivet
paralellkonduktans G = 0.008455 Siemens/km ej uppgivet
då vi rör vid LF-frekvenser så kan vi sätta G = 0 eller kanske
till 0.000001876 för 20000 Hz (speglar förlustvinkel av 0.0003 som är
ganska normalt för plastisolering) och R = 190, det uppgivna
188 Ohm/Km då vi knappast har någon märkbar skin-effekt.
(simulatorn (Microcap ver. 7) kan tyvärr inte ta 'G' parametrar
utan endas R, C och L i sin transmissionsline-simulering
- idiotiskt att en programvara som fullt ut kosta ~ 30000:-
inte klarar det som en öppen-källkods-SPICE klarar, produkten
bygger trots allt på en Spice-snurra i botten...)
Nå, vi får sätta G =0 i fortsatt modulering enligt schema:
<
Loading Image...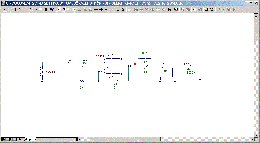
>
-----------------------------------------------------------------------
| längd |100 Hz | 22000 Hz | delta dB 100 Hz - |parallell kond C1|
| | | | 22000 Hz |för kompencering |
-----------------------------------------------------------------------
10 -0.830 dB -0.847 dB -0.017 dB 4.9 nF
20 -0.831 dB -0.899 dB -0.068 dB 10.0 nF
50 -0.836 dB -1,247 dB -0.411 dB 24.9 nF
100 -0.843 dB -2.3 dB -1.459 dB 49.8 nF
500 -0.903 dB -11.49 dB -10.59 dB 298.6 nF
(Med kompenseringskondensator C1 så är frekvensojämnheten mindre än
0.1 dB i hela området mellan 100 - 22000 kHz på de längre
kabelsträckorna.)
Med andra ord oväntat liten skillnad mot ovanstående
RCRCRC simuleringen tidigare
- Här kan man också utläsa en tumregel om ca 5 nF
kompenseringskondensator (C1) per 10 meter Cat-5 kabel
- dock endast vid 1 kOhm matning och 10 kOhm lyssningsimpedans
enligt modellen/schemat.
Här skulle jag också ha satt in pulsutseenderna för resp. längd
- men simuleringstiden är i timmar per plot och det lilla jag har sett
så är det väldigt liten skillnad mot dom tidigare länkarna med
RCRC-simuleringarna - det som märks som skillnad är tidsfördröjningen
för inmatad flank och det som kommer fram i andra ändan på de längre
sträckorna.
----
[1] Utredning Cat-5 kabel:
< http://www.ggriller.co.at/images/pdf/kommleitg_utpc_kat5_030205.pdf >
så utläser jag följande:
Parallellcapacitans (par) : 52 pF/m
resistans - enkel ledare : 94 Ohm/km
loopresistans (par) : 188 Ohm/km
våghastighet : 0.67c
impedans : 100 Ohm +/- 15% (vi antar 100 Ohm)
dämpning 1 MHz : 2 dB/100m
10 MHz : 6 dB/100m
25 MHz : 9.4 dB/100m
31.25 MHz : 10.5 dB/100m
62.5 MHz : 14.7 dB/100m
100 MHz : 18.8 dB/100m
155 MHz : 24 dB/100m
200 MHz : 28 dB/100m
300 MHz : 34 dB/100m
Vi har allt vi behöver - även om man önskade uppgift om längsmed-
induktans - den måste räknas fram baklänges nu.
för att räkna fram kablens primära konstanter (vid 1 MHz)
behöver vi:
frekvens : 1 MHz
faskonstanten beta: 0.67c => 3E8/0.67 = 2.01E8 m/s
=> 2.01E8/1E6 = 201.0 m våglängd
=> 2PI/våglängd = 2PI/201 = 0.03126 rad/m
eller 31.26 rad/km
Dämpning alpha: 2 dBm/100m => 20 dBm/km =>
20/8.686 = 2.3026 neper/km
Impedans Z: som här förutsätts vara reel dvs. 100 |_ 0 grader Ohm
med gamma = alpha + jbeta
___________________
/
och gamma = \ / (r+jwl) * (g + jwc) (w = omega = 2 * PI * f)
\/
_____________
/ r + jwl
samt Z = \ / -------------
\/ g + jwc
i bakhuvudet
så kan man skriva:
gamma * Z = r + jwl
och
gamma
----- = g + jwc
Z
dvs.
alpha = 2.3026 neper/km
beta = 31.26 rad/km
gamma = alpha + jbeta = 2.3026 neper/km + j31.26 rad/km
= 2.3026 + j31.26
r + jwl = gamma * Z = (100 + j0) * (2.3026 + j31.26) = 230.26 + j3126
realdelen:
=> r = 230.26 Ohm
och imaginärdelen:
=> wl = 3126 => L = 3126/2PI*1e6 = 3126/6.283E6 = 0.4975 mH/km
dvs:
längsmedresistansen är 230 Ohm/Km och
längsmedinduktansen är 0.4975 mH/km vid 1 MHz.
OK, capacitans och konduktans då?:
gamma 2.3026 + j31.26
----- = ----------------- = 0.023026 + j 0.3126
Z 100 + j0
g = 0.023026 Siemens (43.4 ohm/km i 'överledning' mellan ledarna vid
1 MHz och representerar en stor del av kabelns
förlust - det är inte utan orsak som man vill
ha skum eller luftisolering i koaxialkablar)
c = 0.3126/2*PI*1E6 = 49.75 nF/km
dvs:
paralellkapacitans är 49.75 nF/km
paralellkonduktans är 0.023026 Siemens/km
OK - jämförelse med kända värden?:
framberäknat @ 1 MHz uppgivet
längsmedresistansen R = 230 Ohm/Km 188 Ohm/km (DC)
paralellkapacitans C = 49.75 nF/km 52 nF/Km
längsmedinduktansen L = 0.4975 mH/km ej uppgivet
paralellkonduktans G = 0.023026 Siemens/km ej uppgivet
längsmedresistansen har högre värden troligen för att
skin-effekten börja göra sig gällande vid 1 MHz.
---
Överkurs:
Koll av skinndjup - en närmeformel för aktiv area på rund ledare
som jag hittade på < http://folk.uio.no/inrf/F1.PDF > är:
2 2 2
PI*R - PI(R - delta) = PI(2*R*delta - delta ) ~= 2*PI*R*delta
__________ _______________
/ 2rho / 1
där delta = \ / ------ = \ / ---------------
\/ wu \/ PI*f*u * sigma
0 0
u = permeabiliteten i materialet
0
1
sigma = -----
delta
rho = resistivteten, typisk 0.0175E-6 rho för koppar
_____________________
/ 2 * 0.0175E-6
vilket blir delta = \ / --------------------- = 66.58E-6
\/ 2*PI*1E6 * 4*PI*1E-7
och applicerat på 0.52 mm diameter för AWG24
så får man 2*PI*R*66.58E-6 = 2*PI*0.00026*66.58E-6
= 107E-9 m2 i effektiv area, 212.4E-9 m2 är den fysiska
arean vilket innebär resistansen är i stort sett
fördubblad vid 1 MHz gentemot DC-loop, men detta
är inget som syns i de beräknade värden - varför ???
strömstrypningen (skin effekt) syns inte i
telegrafekvationerna utan fördelas på
seriereistans R och konduktans G som förlust.
vi provar:
____________________
/ 376 + j 2*PI*1E6*l
Z = \ / ------------------- = 100.4 Ohm |_ -3.2 grader
\/ 0 + j 2*PI**1E6*c
_____________________
gamma = alpha + jbeta = \/ (r + jwl) * (g + jwc) =
______________________________________________
= \/ (376 + j(2*PI*1E6*l)) * ( 0 + j(2*PI*1E6*c)) =
_______________________________
= \/ (376 + j3126) * ( 0 + j0.3126) = 1.877 + i31.32
nu bryr vi endast om alpha = 1.877, realdelen som representerar
dämpningen = 1.877 * 8.686 = 16.3 dB/km - beta - faskonstanten
är stort sett samma som innan.
Trots att vi fördubblade slingresistansen pga. skineffekten
och använder 'perfekt förlustfri isolering så är dämpningen
ändå lägre än den verkliga kabeln.
vidare, för att få ut en troligare 'g' än första ansatsen:
_______ _______
r / c g / l
alpha ~= --- * \ / --- + --- * \ / ---
2 \/ l 2 \/ c
vi har 16.3 dB i dämpning i ideala systemet - men har 20 i verkligheten
enl. tabellen dvs. alpha2 = 20 - 16.3 = 3.7 dB som skall översättas i g
- vi bryr oss endast om sista halvan av ovanstående
______
g / l 2 * alpha2
dvs alpha2 = --- * \ / --- omstuvning => g = ------------
2 \/ c _____
/ l
\ / ---
\/ c
2 * (3.7 / 8.686)
= -------------------- = 0.008455 Siemens (eller 118.3 ohm parallellt)
100.76
nya värden framräknat för 1 MHz
framberäknat @ 1 MHz uppgivet
längsmedresistansen R = 376 Ohm/Km 188 Ohm/km (DC)
paralellkapacitans C = 49.75 nF/km 52 nF/Km
längsmedinduktansen L = 0.4975 mH/km ej uppgivet
paralellkonduktans G = 0.008455 Siemens/km ej uppgivet
(detta förutsätter att vi litar på skin-effekten på koppartråden)
och en koll igen:
___________________________
/ 376 + j 2*PI*1E6*l
Z = \ / -------------------------- = 100.3 Ohm |_ -2.655 grader
\/ 0.008455 + j 2*PI*1E6*c
- ser bra ut, vidare
gamma = alpha + jbeta = \/ (r + jwl) * (g + jwc) =
_____________________________________________________
= \/ (376 + j(2*PI*1E6*l)) * ( 0.008455 + j(2*PI*1E6*c)) =
_______________________________________
= \/ (376 + j3126) * ( 0.008455 + j0.3126) = 2.3 + j31.29
och alpha är 2.3 * 8.686 = 19.98 dB - som önskat :-)
----
En ganska lång text, hoppas att någon orka läsa hit
- eller åtminstone den första halvan :-)
Med sedvaliga reservationer för skrivfel och räknefel och
därav kanske helt tokiga följdresultat - även om jag har
försökt ha haft en smula reality-check på slutsatserna :-)
/TE